Atcoder Beginner Selectionを時初めてから約3日くらい経ってようやく最後の問題であるTravelingまで終わりました。
今回はこの問題を解くために使ったアイデアを簡単に紹介したいと思います。
Travelingの問題文:https://atcoder.jp/contests/abs/tasks/arc089_a
全体のコード
#include <iostream>
#include <vector>
#include <string>
using namespace std;
bool arrive(int x1, int y1, int x2, int y2, int move_num)
{
bool result = false;
int diff = abs(x1 - x2) + abs(y1 - y2);
if (diff > move_num)
return result;
if ((move_num - diff) % 2 == 0) // come and back. the diff can be ignored.
result = true;
return result;
}
int main()
{
int N;
cin >> N;
vector<int> x(N + 1);
vector<int> y(N + 1);
vector<int> t(N + 1);
for (int i = 1; i < N + 1; ++i)
cin >> t[i] >> x[i] >> y[i];
bool can_arrive;
for (int i = 0; i < N; ++i)
{
can_arrive = arrive(x[i], y[i], x[i + 1], y[i + 1], abs(t[i + 1] - t[i]));
if (!can_arrive)
break;
}
if (can_arrive)
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}問題と解くのに使った考え方
まず、二点A、Bを用意します。

次にAからBの距離を測ります。この問題の場合は一度に動ける範囲が1つだけなので、距離はA、Bのx座標とy座標の差に対して絶対値を取ったものの合計値で表せます。
int diff = abs(x1 - x2) + abs(y1 - y2);
次に、求めたdiffと動くことのできる回数(以下move_num)を比べます。動くことのできる回数とは、問題文で与えられているtのことです。
もし、diffよりもmove_numが小さいなら、どうやってもAからBに到達することはできません。なのでこの時点で答えはNoになります。
そうじゃない場合はとりあえずAからBに到達はできることになります。
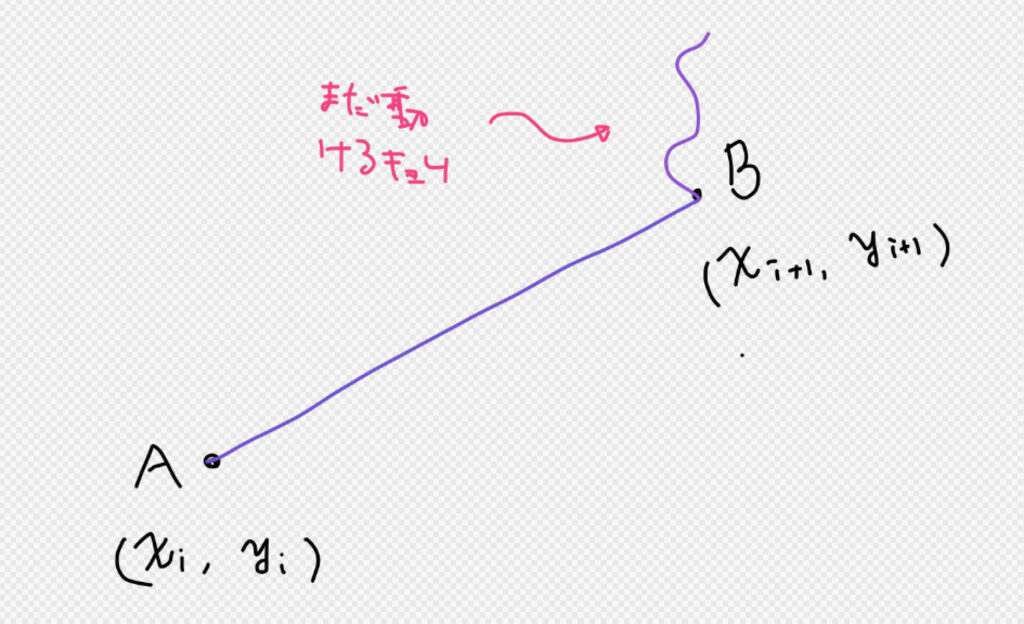
最後はまだ動けるキョリ( move_num – diff )が奇数であるか偶数であるか考えるだけです。偶数の場合は答えはYes、奇数の場合はNoになります。
なぜなら偶数の場合はまだ動けるキョリをBから1歩行って、また戻る作業を使って消化できるからです。奇数でそれをすると最後に一歩だけ余っちゃいます。
